【R】包絡分析（DEA)や確率フロンティア分析（SFA)のRパッケージ: Benchmarking

包絡分析（Data Envelopment Analysis) や確率フロンティア分析（Stochastic Frontier Analysis）は企業や団体の生産性・効率性を測るのに使用される分析方法である。

入力（input）と出力（output）について、クロスセクション（一時点で複数の企業等のデータ）、時系列（一つの企業等のデータで複数時点）、パネルデータ（複数時点で複数の企業等のデータ）などを所与として、最も効率的な入力と出力の関係を推定・計算し、さらに各企業や時点での生産がその効率的な生産関係に比べてどの程度非効率かを計算する。

日本語での文献は知らなかったのだけれど、割と企業などでも一般的に使われている手法らしい。学術論文でも使われてはいるが、経済学の最新の論文とかではなくもっと応用分野で使われている印象。技術として実務で使われている印象がある。

包絡分析 DEA

DEAは線形計画法の応用であり、データを所与としてフロンティアを推定し、それぞれのデータポイントの効率性をフロンティアとの距離の割合で計算する。

効率性の測り方にはいくつかあるが、主なものとして入力型と出力型がある。(Input-orientedとOutput-oriented)
例えば出力型で例えると、企業Aは10人の人員で10個のコーヒーを作ったとする。企業Bは同じ人員で8個のコーヒーを作ったとする。
すると、同じ投入量で産出量が違い、企業Aの産出量がデータ（この場合n=2)の中で最大なので、企業Aの効率性指標は1であり「効率的」、企業Bは0.8で非効率、または投入量を増やさずに算出を増やす余地があると考える。（人員以外の入力はこの例では無視しているが、実際の推定ではもちろん考慮する。）

数学的な説明はここでは省略するが、「包絡分析」でググると解説記事(刀根,1996)やその他の説明記事がヒットする。

英語が読める方はCoelli et al (2005)やBogetoft and Otto (2011)がよい本だと思う。特に後者はここで説明するBenchmarkingパッケージのもとになっている本でRでの説明がなされている。

DEA 関数

BenchmarkingパッケージはCRANからインストールできる。

まずは例となっているデータを見てみよう。特に統計的分析するわけではないので観察数は少ない。

# library
library(Benchmarking)

# Data 1
# input vector
  x <- matrix(c(100,200,300,500,100,200,600),ncol=1)
  
# Output vector
  y <- matrix(c(75,100,300,400,25,50,400),ncol=1)

Benchmarkingに入っている関数で入力と出力の関係をプロットしてみる。
以下ではフロンティアを描くためにdea.plot.frontier関数を使っているが、等産出量曲線を描くdea.plot.isoquant(x1,x2,....)や2財（出力）の間の生産可能フロンティアを描くdea.plot.transform(y1,y2,....)も用意されている。

# Plot
 dea.plot.frontier(x,y,txt=TRUE)

f:id:keita43a:20190710205522p:plain

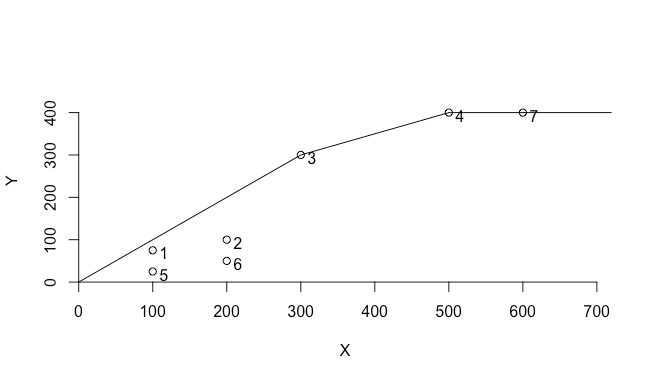
X軸が入力、Y軸が出力である。
そして最も外側に位置するデータ点を結ぶように線が引かれているが、これが日本でいうと包絡、英語で言うEnvelopeであり、生産フロンティアとなる。データ点2や6はフロンティアの内側にあり、これらの点は非効率ということになるが、他の点も定義によっては非効率になりうる。

また、この包絡線は仮定する技術によっても異なる。デフォルトでは規模によって収穫可変となっており、もっともタイトに包絡線を描くが、例えば規模に対して収穫逓減を仮定すると下図のようになる。

# Plot decreasing return to scale
 dea.plot.frontier(x,y,txt=TRUE, RTS = "drs")

f:id:keita43a:20190710211138p:plain

技術の仮定を変更するにはRTSという引数を変更する。デフォルトは"vrs"で収穫可変だが、"crs"収穫一定、"irs"収穫逓増, "irs2"収穫逓増だが凸性を仮定しない、などが指定できる。

問題はどれぐらい非効率か？ということだが、上述のように効率性の定義によって異なる。
入力型だと、出力を固定して、入力がいかに低いか？となり、投入量の比として計算されるが、出力型だと入力を所与として出力の量の比になる。

Benchmarkingパッケージのdea関数でどちらも推定することができる。
dea関数の中でORIENTATIONという引数を"in"にすれば入力型、"out"にすれば出力型である。

# Estimation
e <- dea(x,y, RTS = "drs", ORIENTATION="in")

> # Efficiency score
> eff(e)
[1] 0.7500000 0.5000000 1.0000000 1.0000000 0.2500000 0.2500000
[7] 0.8333333

上の結果は収穫逓減を仮定して入力型で推定した結果である。
たとえば点１は0.75と出ているが、これは点１におけるY（出力）の量（＝75)を算出するには、推定されたフロンティアによれば必要最低限な量は75で実際に点１で投入されている量は100なので75/100の0.75が効率性指標となる。これが1に近ければ近いほど効率的であり、入力型の場合は非効率であれば「入力を使いすぎ」という解釈の仕方ができる。

出力型であればORIENTATIONを"out"にして

# Estimation
e <- dea(x,y,RTS = "drs",ORIENTATION="out")

> # Efficiency score
> eff(e)
[1] 1.333333 2.000000 1.000000 1.000000 4.000000 4.000000 1.000000

すると点１は1.333333となっている。これは点１の入力量である100を投入したならば推定されたフロンティアによれば100の出力ができるはずなのに実際に観察された出力は75なので100/75 = 1.3333となっている。つまりどれぐらい「出力しなさすぎ」なのかという指標であり、数字が大きければ大きいほど非効率、1に近いほど効率的である。

観察数が少なければ一つ一つ見ることも可能だが、多くのデータを持っていて要約をみたい場合はsummary関数が使える。

> # Result summary
> summary(e)
Summary of efficiencies
DRS technology and output orientated efficiency
Number of firms with efficiency==1 are 3 out of 7 
Mean efficiency: 2.05 
---                
  Eff range      #  %
       F ==1     3 43
    1< F =<1.1   0  0
  1.1< F =<1.2   0  0
  1.2< F =<1.3   0  0
  1.3< F =<1.5   1 14
  1.5< F =<  2   1 14
    2< F =<  5   2 29
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.000   1.000   1.333   2.048   3.000   4.000

どの範囲にいくつ観察点が含まれているかという要約になる。
F==1の効率的な点は3つあり、全体の43%。一方でFが2以上の比較的非効率な点は2つあるという感じです。

複数の入力

当然ですが、複数の入力・出力がある場合がほとんどですが、それも対応しています。
引数に入れるxやyをベクトルから行列にするだけです。

  # input vector
  x <- matrix(c(100,200,300,500,100,200,600),ncol=1)
  x2 <- matrix(c(200,100,400,200,400,300,200),ncol=1)
  xx <- cbind(x,x2)

ただし、図を描くときはそのまま入れるとなぜか各行を合計した値を使ってしまうので、描きたい変数の列を指定する必要があります。

# Plot
  dea.plot.frontier(x[,1],y,txt=TRUE,RTS = "drs")

確率フロンティア分析 (SFA)

確率フロンティア分析はDEAに比べてより統計的・計量経済学的で、その大きな特徴は

確率的ノイズを考慮に入れる
生産関数の関数形を特定化する

ところにあります。

Coelli et al (2005)によれば、DEAに比べて確率的なモデルにすることで不要なノイズをフロンティア推定に含めない点と統計的な仮説検定ができる点を利点として挙げていますが、一方で非効率性の確率分布や関数形の特定化が必要なところが弱点としています。

こちらも詳細な説明はほぼ省きますが簡単にいうと

$y = f(K,L) - u + v$

という生産関数を仮定します。 $y$ が出力（生産量）、 $f(K,L)$ が投入量の関数で、 $u$ が技術的非効率性、 $v$ がノイズです。

投入量の関数のところはが「関数の特定化」が必要なところで、コブ=ダグラス型だったり、トランスログ関数だったりするのが一般的です。

$u$ の技術的非効率性というところがキーで、この部分に0以上の値を取る確率分布を仮定します。この部分が非効率性として推定されます。

$v$ の部分は一般的な回帰分析と同じように撹乱項です。

sfa関数

Benchmarkパッケージではsfa関数が用意されています。
入力を右辺の説明変数として行列で与え、出力をベクトルで与えます。
今気づいたけど、これは行列でxを与えなくてはいけないのでトランスログなどの関数形にする場合は自分で行列を作ってやらないといけないみたいですね。ここではx1とx2をそのままナイーブに与えています。

uの分布として0以上正の数をとる半正規分布を仮定しています。

# data making

n <- 50
x1 <- 1:50 + rnorm(50,0,10)
x2 <- 100 + rnorm(50,0,10)
x <- cbind(x1,x2)
y <- 0.5 + 1.5*x1 + 2*x2 + rnorm(n,0,1) - pmax(0,rnorm(n,0,1))


# Plot
plot(x1,y)
plot(x2,y)

# Estimation
sfa_model = sfa(x,y)

summary()関数で回帰分析と同じように結果を見れます。
違うのは、sigma2vでノイズの分散を、sigma2uで効率性の項の半正規分布の分散を表示しています。
ラムダ(lambda)は効率性項の分散とノイズの分散の比、のはずなんですが、なぜか数字が合いません。

> summary(sfa_model)
            Parameters   Std.err   t-value  Pr(>|t|)
(Intercept)     -1.246   2.20999   -0.5639     0.575
xx1              1.493   0.01146  130.2983     0.000
xx2              2.029   0.02018  100.5718     0.000
lambda           2.055   1.03982    1.9767     0.054
sigma2         3.8845 
sigma2v =  0.7434977 ;  sigma2u =  3.140989 
log likelihood =  -85.76285 
Convergence =  4 ; number of evaluations of likelihood function 23 
Max value of gradien: 0.1215212 
Length of last step: 0 
Final maximal allowed step length: 0.33075

この結果、推定された係数のうち、uとeをのぞいてフィットした関数がSFAで推定されたフロンティアということになります。

plot(x1,y)
abline(a=coef(sfa_model)[1] + coef(sfa_model)[3]*mean(x2), 
       b=coef(sfa_model)[2],col = "red")

f:id:keita43a:20190710225112p:plain

図のように、赤線がフロンティアですが、いくつかの観察点はフロンティアの外に出ています。
これはノイズの結果がフロンティアの外に出ているということで、システマティックな結果ではないという解釈になります。
DEAだとこういった結果もすべてフロンティアの内側に入れてしまうので、DEAの方がフロンティアが外側に位置することになり、結果的に
非効率性も大きく計算されがちです。

まとめ

効率性の分析において使われる2つの推定方法、DEAとSFAを簡単にRで行いました。
一番新しいパッケージはこのBenchmarkなのですが、DEAに寄っていてSFAの方はDEAの結果と比較するために簡単に付属している、という印象です。
SFAによる分析のためのRパッケージはCoelliが開発したFRONTIERというFortranによるプログラムをRに移植したfrontierパッケージのほうが秀でている気がしますので、別記事で（時間があれば/必要に応じて）書こうと思います。
DEAについてももう少し深めて書く時間が取れれば書き足す予定です

RでのDEAについての本（洋書）が出たようです。（お高い・・・）