Waves, Currents and Insights

旧データ分析メモと北欧生活。データ分析、計量経済・統計とR、水産資源管理、英語勉強、海外生活などについて備忘録や自分の勉強のOutputの場所として

MENU

回帰分析で対数変換などもう古い、時代は逆双曲線正弦変換だ！

計量経済学 データ分析 R

みたいなキャッチーなタイトルを書いてみたけれど、自分もつい最近共著者から聞いて知った。
応用実証経済学の最前線にいる人は当然知ってるっぽくて、冷や汗かいた話です。

端的に言えば、回帰分析において弾力性を計るために、対数変換じゃなくて、最近は逆双曲線変換をするのがよいらしい。

記事を書き上げてから「先行文献」をサーチしていたら、さすがのhimaginary先生のブログポストがすでにありました…
himaginary.hatenablog.com

元ネタはミネソタの有名な農業経済・応用経済学者のMarc Bellemareのこの記事のようですが、
本記事はその後BallemareとGeorgia TechのCathy J. Wichmanが書いた論文に基づいています。以下の論文に基づいて、あくまでざっくり説明するので、もし使ってみる場合はぜひ論文を読んでください。

Elasticities and the Inverse Hyperbolic Sine Transformation - Bellemare - 2020 - Oxford Bulletin of Economics and Statistics - Wiley Online Library

回帰分析における弾力性の推定


keita43a.hatenablog.com


以前、上のような記事を書いたのだけれど、この記事では4つ目の弾力性を測るところに該当する。

対数変換の一番大きな問題は、元の値が0のときに定義できないことだ。 \ln (0)は定義できない。

なので、０が多いデータなどであれば実務的には任意の小さな数を足して対数をとったりすることがある。

近似としては問題ないだろうということで使われてきたが、当然ながら元のデータをいじっていることになってしまう。

そこで、最近では逆双曲線サイン関数 (Inverse hyperbolic Sine) を使う研究が経済学の実証で増えている。
その理由は、1) 対数に似ている。2) 0が定義できる　の２つである。



逆双曲線正弦関数

逆双曲線関数 - Wikipedia

Wikipediaにもあるとおり、逆双曲線正弦（サイン）関数は以下のように定義される。

arsinh(x) = \ln (x + \sqrt{x^2 + 1})


ちなみに、逆双曲線正弦関数は arcsinh(x)や、 sinh^{-1}(x)という表記もあるが、同じものである。ここでは arsinh(x)で統一する。

まぁ確かに、 x=0のときに、 arsinh(0) = \ln(1)になるので、元の変数が0をとっても定義できる。

弾力性の導出

本当に弾力性が導出できるのかよ？
というわけで、回帰式の両辺の変数を変換した式から導出してみよう。

以下のような式を考える。

arsinh(y) = \alpha + \beta arsinh(x) + \varepsilon

このとき、元の被説明変数 yは

y = sinh(\alpha + \beta arsinh(x) + \varepsilon)

と逆関数である双曲線サイン関数で表現できる。

そして、これをxについて微分すると

\frac{\partial y}{\partial x} = \frac{\beta cosh(\alpha + \beta arsinh(x) + \varepsilon)}{\sqrt{x^2 + 1}}

となる。ここでは、 sinh(x)の導関数は cosh(x)であることと、 arsinh(x)の導関数が \frac{1}{\sqrt{x^2 + 1}}であることを利用している。

この微分を弾力性の定義に当てはめると、

\frac{\partial y}{\partial x}\frac{x}{y} = \frac{\beta cosh(\alpha + \beta arsinh(x) + \varepsilon)}{\sqrt{x^2 + 1}}\cdot\frac{x}{y}

cosh(\cdot)の中身が、回帰式なので左辺 arsinh(y)で置き換えると

\frac{\beta cosh(arsinh(y))}{\sqrt{x^2 + 1}}\cdot\frac{x}{y}

となる。

ここで、 cosh^2(x) - sinh^2(x) = 1という恒等式と、逆関数なので sinh(arsinh(x))=xであることを利用すると、

cosh(arsinh(y)) = \sqrt{1 + sinh^2(arsinh(y))} = \sqrt{y^2 + 1}

であるので、元の弾力性の式は

\frac{\partial y}{\partial x}\frac{x}{y} = \beta\frac{\sqrt{y^2 + 1}}{y}\cdot\frac{x}{\sqrt{x^2 + 1}}

となる。

このとき、
\lim_{y \rightarrow \infty} \frac{\sqrt{y^2 + 1}}{y} \approx 1
\lim_{x \rightarrow \infty} \frac{x}{\sqrt{x^2 + 1}} \approx 1

となるので、yとxの数値がそれぞれある程度大きいときに、

\frac{\partial y}{\partial x}\frac{x}{y} \approx \beta

として、推定されたパラメターを弾力性として解釈できる。

問題点

弾力性として使えそうだが、やはりパーフェクトではない。
問題は「ある程度大きいときに」という点だ。

Bellemare & Wichmanでは、数値が10より大きければ誤差は0.5%程度になり大きな問題ではないだろうとしている。

しかし、そもそも対数ではなく逆双曲線サイン関数を使う理由はゼロ値を取れることがモチベーションだった。
もし0の割合が小さいデータならあまり問題にならないが、もし大きければ近似による誤差が大きくなってしまう。

そこで、もし0の割合がある程度大きい場合は、 \betaの推定値そのものを解釈するのではなく、導出された弾力性そのものを使って計算するのが望ましい。
たとえば、元のデータの平均値を使って、以下のように平均値における弾力性を報告する。


\frac{\partial y}{\partial x}\frac{\bar{x}}{\bar{y}} = \beta\frac{\sqrt{\bar{y}^2 + 1}}{\bar{y}}\cdot\frac{\bar{x}}{\sqrt{\bar{x}^2 + 1}}

シミュレーション

Bellmare & Wichmanではモンテカルロシミュレーションによって、数値が小さい場合にどうなるかを評価している。
一応Rコードでそれをリプリケートしてみた。Stataユーザーの方は、著者のCathy J. Wichmanがコードを公開してくれているので参照されたい。

結果を先に書くと、このような形になった。乱数生成のプロセスが入っているので、論文のTable 1と全く同じにはなっていないが、傾向は同じである。

Table 1: 弾力性の推定値

ついでに、弾力性だけではなく回帰分析の推定値自体でもテーブルを作ってみた。

Table 2: 係数の推定値

いずれも、arcsinh-arcsinhのときには、k=10を超えたあたりから推定値が安定しているのがわかる。

また、k->0のときに、推定値がlinear-linearの推定値に近づいていっているのも特徴である。
このように値が小さかったり、0を取る数値が多い場合にも頑健な推定ができるのがこのアプローチのいいところであるとのこと。

推定に使ったRコードは以下。

# 再現性のためにランダムシードを設定
set.seed(12345)

# 1000個の観測値を持つサンプルデータを作成
n <- 1000
x <- rnorm(n, mean = 10, sd = sqrt(2))
y <- 5 + 0.5 * x + rnorm(n, mean = 0, sd = sqrt(2))

# 変換変数を生成
xbar <- mean(x)
ybar <- mean(y)
ihs_y <- asinh(y)
ihs_x <- asinh(x)

# 各k値に対する変数のスケーリングバージョンを作成
k_values <- c(0.001, 0.01, 0.5, 1, 5, 10, 50, 100, 1000, 10000)  # フルテーブルに合わせて小さいk値を追加
transformed_data <- list()

for (i in k_values) {
  transformed_data[[paste0("ihs_y_", i)]] <- asinh(y * i)
  transformed_data[[paste0("ihs_x_", i)]] <- asinh(x * i)
  transformed_data[[paste0("y_", i)]] <- y * i
  transformed_data[[paste0("x_", i)]] <- x * i
  transformed_data[[paste0("ybar_", i)]] <- ybar * i
  transformed_data[[paste0("xbar_", i)]] <- xbar * i
}

# ベータと弾力性の両方の結果を格納するための行列を作成
beta1 <- numeric(length(k_values))
beta2 <- numeric(length(k_values))
beta3 <- numeric(length(k_values))
beta4 <- numeric(length(k_values))
m1 <- numeric(length(k_values))
m2 <- numeric(length(k_values))
m3 <- numeric(length(k_values))
m4 <- numeric(length(k_values))

# モデル1: 標準弾力性（y on x）
for (j in 1:length(k_values)) {
  i <- k_values[j]
  model <- lm(transformed_data[[paste0("y_", i)]] ~ transformed_data[[paste0("x_", i)]])
  beta1[j] <- coef(model)[2]  # ベータ係数を保存
  m1[j] <- beta1[j] * transformed_data[[paste0("xbar_", i)]] / transformed_data[[paste0("ybar_", i)]]
}

# モデル2: y on IHS(x)
for (j in 1:length(k_values)) {
  i <- k_values[j]
  model <- lm(transformed_data[[paste0("y_", i)]] ~ transformed_data[[paste0("ihs_x_", i)]])
  beta2[j] <- coef(model)[2]  # ベータ係数を保存
  m2[j] <- (beta2[j] * transformed_data[[paste0("xbar_", i)]]) / 
    (transformed_data[[paste0("ybar_", i)]] * sqrt(transformed_data[[paste0("xbar_", i)]]^2 + 1))
}

# モデル3: IHS(y) on x
for (j in 1:length(k_values)) {
  i <- k_values[j]
  model <- lm(transformed_data[[paste0("ihs_y_", i)]] ~ transformed_data[[paste0("x_", i)]])
  beta3[j] <- coef(model)[2]  # ベータ係数を保存
  m3[j] <- beta3[j] * transformed_data[[paste0("xbar_", i)]] * 
    (sqrt(transformed_data[[paste0("ybar_", i)]]^2 + 1) / transformed_data[[paste0("ybar_", i)]])
}

# モデル4: IHS(y) on IHS(x)
for (j in 1:length(k_values)) {
  i <- k_values[j]
  model <- lm(transformed_data[[paste0("ihs_y_", i)]] ~ transformed_data[[paste0("ihs_x_", i)]])
  beta4[j] <- coef(model)[2]  # ベータ係数を保存
  m4[j] <- (beta4[j] * transformed_data[[paste0("xbar_", i)]] * 
              sqrt(transformed_data[[paste0("ybar_", i)]]^2 + 1)) / 
    (transformed_data[[paste0("ybar_", i)]] * sqrt(transformed_data[[paste0("xbar_", i)]]^2 + 1))
}

# 弾力性とベータのための結果テーブルを作成
elasticity_results <- data.frame(
  k = k_values,
  linear_linear = m1,
  linear_arcsinh = m2,
  arcsinh_linear = m3,
  arcsinh_arcsinh = m4
)

beta_results <- data.frame(
  k = k_values,
  linear_linear = beta1,
  linear_arcsinh = beta2,
  arcsinh_linear = beta3,
  arcsinh_arcsinh = beta4
)

# フォーマットされたテーブルを表示
options(scipen = 999)  # 科学的表記法を無効化
cat("弾力性の推定値:\n")
print(round(elasticity_results, 6))

cat("\nベータ係数:\n")
print(round(beta_results, 6))




経済学の数学は三角関数いらないよ！って言われて勉強してこなかったんですけど…という気持ち。





余談ですが、Bellemareさんといえばこんな本を最近出されましたね。

Doing Economics: What You Should Have Learned in Grad School―But Didn’t

Doing Economics: What You Should Have Learned in Grad School―But Didn’t

Amazon

Macでggplot2を日本語でPDF出力する

R 備忘録

Macでggplot2を使って日本語PDF出力をするのに、生成AIに聞いたりして色々やってみたがエラーを吐く（うまく日本語が表示されない）ので検索して調べた結果、こちらの記事の中にある記述で解決した。

ill-identified.hatenablog.com


ggsave()の引数にdevice=quartzと指定することで日本語フォントを含んでいても出力できる。

p <- ggplot(...) + ...

ggsave("...pdf", plot=p, device = quartz, type = "pdf")

ggplot日本語化の問題

ggplot2で日本語で描画するときに、macではきちんとフォントを指定しないと豆腐化する（文字化けして□になる）は知られた問題である。

library(tidyverse)

# 図の例：mtcarsでシリンダーの数と燃費を比較
p <- ggplot(mtcars, aes(x=cyl,y = mpg, fill = factor(cyl))) + 
  geom_boxplot() +
  labs(x = "シリンダー数", y="燃費（ガロンあたりのマイル）",
       fill="シリンダー数")

p
豆腐化したggplot


theme_bw(base_family="...")とかtheme(text = element_text(family = "..."))でフォントを指定すると解決する。

# library
library(tidyverse)
library("systemfonts")

# システム上で使える日本語フォントのリストを探す
japanese_fonts <- system_fonts() |> 
        filter(grepl("Hira|JP|Japanese|Gothic", family)) |>
        pull(family) |>
        unique()
      
# 日本語フォント一覧の表示
print(japanese_fonts)


# 修正した図の例：mtcarsでシリンダーの数と燃費を比較
p <- ggplot(mtcars, aes(x=cyl,y = mpg, fill = factor(cyl))) + 
  geom_boxplot() +
  labs(x = "シリンダー数", y="燃費（ガロンあたりのマイル）",
       fill="シリンダー数")+
  theme(text = element_text(family = "Hiragino Sans"))

p
豆腐化を解決した図

ggplot日本語化のpdf出力問題

ggsave()を使って、pdf出力するときにきちんと日本語が表示されなかった。

ggsave("シリンダーと燃費.pdf",
       plot = p,
       device="pdf")

Error in grDevices::pdf(file = filename, ..., version = version) : 
  unused argument (type = "pdf")

出力されたファイルを見ると、文字があるべきところが真っ白になっている。

以下のようにdeviceにquartzと指定すると、きちんと日本語が表示される。

ggsave("シリンダーと燃費.pdf",
       plot = p,
       device=quartz,
       type="pdf")

元記事では、MacでもX11(Xquartz)をインストールして、cairo_pdf()を使うことが推奨されているが、とりあえず出力したい場合はこの方法が一番簡単そう。

コリン・クラークの水産経済学への貢献

水産資源管理

On The Contribution Of Colin Clark to Fisheries Economics （Colin Clarkの水産経済学への貢献について）というタイトルでGordon Munro先生のスピーチがアップされていたので拝見した。


背景知識として、水産経済学ではColin ClarkとGordon Munroはどちらもカナダのブリティッシュ・コロンビア大学の名誉教授で、ふたりともいわゆる大御所である。
水産資源の経済学に自然資本という概念を導入して、動学的な分析の基礎を築いたのはこの二人である。
コリン・クラークは数学者で、ゴードン・ムンロは経済学者であるが、ゴードンによれば当時の数学的なスキルは当然数学者のほうが進んでいて、そのスキルが水産資源の経済理論を発展させるのに大きく貢献したという。

残念ながらコリン・クラークは今年の４月に亡くなってしまった。92歳であった。
ゴードン・ムンロも90歳を超えているが、未だに研究をしていて海外学会で発表している。
今年7月にマレーシアであった学会でもお見かけした。筆者はムンロ先生とは面識があるので少し話したが、研究の話がポンポン出てきて未だに第一線にいる感じである。


大まかなスピーチの内容はざっとこんな感じ。

1. もっとも重要な貢献として、水産資源を資本として扱い、どのようなストックが最適なのか？という問題を数学的に扱う方法を開発した。

関連論文は以下のClark and Munro (1975)。
www.sciencedirect.com

2. すべての水産資源経済学のモデルは、生物学的モデルに依拠している。

生物学のモデルに依拠した経済モデルを開発した貢献が大きい。
どの程度のスピードで資源を収穫できるかは、生物資源の再生速度に依拠する。

ClarkはMathematical Bioeconomicsという書籍を書いている。一番新しいのは以下の第３版だろう。

Mathematical Bioeconomics: The Mathematics of Conservation (Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts)

Mathematical Bioeconomics: The Mathematics of Conservation (Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts)

Amazon

3. 実際の水産管理においては、不確実性や不均等な漁業資源の分布などを考慮しないといけない。

当然ながら数学的に単純化されたモデルがそのまま様々な漁業に当てはまるわけではない。
しかし、資源を資本として考えて、きちんと管理すれば将来にわたって社会全体に利益をもたらすということを理解することが重要である。


今では当たり前に聞こえるような概念でも、先人がその概念を提唱し、それを厳密に理論として分析してきたから今の議論がある。


コリン・クラークの貢献については、Environmental and Resource Economics誌にもムンロとUBCの水産経済学者であるU. Rashid Sumailaによる記事が寄稿されている。
link.springer.com

日本の排他的経済水域の地図データ


仕事で日本の排他的経済水域の地図データを探していたのだが、日本の国土地理院の数値データ
（国土数値情報ダウンロードサービス）などは見当たらなかった。

日本の排他的経済水域は、海上保安庁のウェブサイトではこういう形になっている。

海上保安庁　日本の領海等概念図

しかし、実際はいくつかの係争中水域や共同開発区域が存在する。

Rには、MazamaSpatialUtilというパッケージがあり、EEZの地図データが含まれている。

それによると、日本のEEZと係争中のエリアを区分けすると次のようになる。


# library
pacman::p_load(
  tidyverse,
  sf,
  rnaturalearth,
  patchwork
)


# Use function
`%!in%` <- Negate(`%in%`)


# Japan land
japan_sf <- ne_countries(country = c('japan','russia','south korea','north korea','china','taiwan','united states of america'),scale="large", returnclass = "sf") %>%
  st_transform(crs=4326)


# EEZ from MazamaSpatialUtils
eez_sf=MazamaSpatialUtils::SimpleCountriesEEZ %>% 
  st_as_sf() %>%
  st_transform(crs=4326) %>%
  filter(countryName %in% c("Japan","South Korea","China","Taiwan","Russia")) %>%
  filter(polygonID %!in% c(22,100,189,33)) # remove mainland China

# test plot of EEZ
ggplot(data=eez_sf) +
  geom_sf(fill="lightblue") + 
  geom_sf(data=japan_sf) +
  #geom_sf_label(aes(label=polygonID)) +
  theme_bw() +
  lims(x=c(120,160),y=c(15,48))


見比べてみると、韓国との暫定水域について、日本の概念図では竹島を日本側に含むラインがあるが、このデータでは存在しない事がわかる。
すなわち、「暫定水域」を定義するラインが存在しない。


EEZのデータは、他にMarine Regionsというウェブサイトで取得することができる。

このウェブサイトでは、EEZのデータについてバージョンが３つ存在する。
Version 1は2012年, Version 2は2014年, Version 3は2020年にリリースされている。


このうち、Version 2と3をダウンロードし、MazamaSpatialUtilのデータと比較してみた。

Marine Regions のEEZ Ver 2, Ver 3を重ねたデータ

すると、MazamaSpatialUtilのデータと、Version 3のデータは一致しているが、Version 2とは異なることが示された。


以下が描画に使用したコードである。

eez_sf_v2 = st_read("EEZ_land_union_v2_201410/EEZ_land_v2_201410.shp") %>%
  filter(str_detect(Country,"Japan")|str_detect(Country,"South Korea")|str_detect(Country,"Russia")|str_detect(Country,"China")) %>%
  st_transform(4326)
  
# Marine Regions ver 3
eez_sf_v3 = st_read("EEZ_land_union_v3_202003/EEZ_Land_v3_202030.shp") %>%
  filter(SOVEREIGN1 %in% c("Japan","South Korea","Russia","China")|SOVEREIGN2 %in% c("Japan","South Korea","Russia","China")|SOVEREIGN3 %in% c("Japan","South Korea","Russia","China")) %>%
  st_transform(4326)

# plot of EEZ: version 2 + version 3 comparison around Takeshima
plot_v2_v3_nationwide = ggplot() +
  geom_sf(data=eez_sf_v2,fill="transparent",col="blue") +
  geom_sf(data=eez_sf_v3,fill="transparent",col="red") +
  geom_sf(data=eez_sf,fill="transparent",col="green",linetype=2) +
  geom_sf(data=japan_sf) +
  annotate(geom = "text",label="Marine Regions version 2", x=142,y=20,col="blue",hjust=0) +
  annotate(geom = "text",label="Marine Regions version 3", x=142,y=19,col="red",hjust=0) +
  annotate(geom = "text",label="MazamaSpatialUtils", x=142,y=18,col="green",hjust=0) +
  labs(title="Marine Regions EEZ data: version 2 & 3") +
  lims(x=c(120,158),y=c(15,48)) +
  theme_minimal()

plot_v2_v3_nationwide


日本海を拡大すると、次のようになる。


# plot of EEZ: version 2 + version 3 comparison around Takeshima island
plot_v2_v3 = ggplot() +
  geom_sf(data=eez_sf_v2,fill="transparent",col="blue") +
  geom_sf(data=eez_sf_v3,fill="transparent",col="red") +
  geom_sf(data=eez_sf,fill="transparent",col="green",linetype=2) +
  geom_sf(data=japan_sf) +
  annotate(geom = "text",label="Marine Regions version 2", x=137,y=33,col="blue",hjust=0) +
  annotate(geom = "text",label="Marine Regions version 3", x=137,y=32.5,col="red",hjust=0) +
  annotate(geom = "text",label="MazamaSpatialUtils", x=137,y=32,col="green",hjust=0) +
  labs(title="Marine Regions EEZ data: version 2 & 3") + 
  lims(x=c(125,145),y=c(32,42)) +
  theme_minimal()

plot_v2_v3


Version 2では、韓国との暫定水域とみられるものがデータとして記録されている。

そのため、冒頭の「日本の領海等概念図」に近い地図データを得るためにはMarine RegionsのVersion 2を利用すると可能となる。



 # 日本が入るポリゴンの抽出
  eez_sf1= st_read("data/raw/EEZ_land_union_v2_201410/EEZ_land_v2_201410.shp") %>%
    filter(str_detect(Country,"Japan")) %>%
    st_transform(4326)
  
 # ポリゴンを結合
  eez_sf2 = eez_sf1%>%
    st_union()
  
      # test plot of EEZ (polygon separated)
      ggplot() +
        geom_sf(data=eez_sf1,fill="lightblue") +
        geom_sf(data=japan_sf) +
        geom_sf_label(data=eez_sf1,aes(label=OBJECTID)) +
        lims(x=c(120,157),y=c(18,48)) +
        theme_minimal()

      # test plot of EEZ (combined)
      ggplot() +
        geom_sf(data=eez_sf2,fill="lightblue") +
        geom_sf(data=japan_sf) +
        lims(x=c(120,157),y=c(18,48)) +
        theme_minimal()


なぜVersion 2からVersion 3への変更について、境界線がこのようになっているかはわからない。

【R】n番目に大きい値をdplyr::summariseする。

データ分析 R R 備忘録

問題

グループごとに平均や最大値などを計算するのに便利なdplyr::summariseですが、たとえば2番めに大きい値を計算したい、というときはどうすればいいか？

解決策

自分で簡単な関数を書く。

max2 <-  function(x) {
      u <- unique(x)
      sort(u, decreasing = TRUE)[2L]
    }

解説

準備

標準装備mtcarsのデータを例に使います。

# パッケージ
library(tidyverse) # dplyr含む

# データロード
data(mtcars)

ステップ１：最大とか

オートマ/マニュアル別に一番いい燃費はいくらか？

> mtcars %>% group_by(am) %>% summarise(mpg_max = max(mpg), mpg_mean = mean(mpg))
# A tibble: 2 × 3
     am mpg_max mpg_mean
  <dbl>   <dbl>    <dbl>
1     0    24.4     17.1
2     1    33.9     24.4


最大だとオートマは24.4、マニュアルは33.9、単位はそれぞれガロンあたりのマイルです。

ステップ２：関数を書く

dplyrにはslice_max(旧top_n)という関数があるのですが、これは大きい方からn個を引っ張ってくる関数です。
n番目だけ（たとえば2番めだけ）を引っ張ってきたいならいっそ関数書いてしまったほうが早そう。

max2 <-  function(x) {
      u <- unique(x)
      sort(u, decreasing = TRUE)[2L]
    }

> mtcars %>% group_by(am) %>% summarise(mpg_max = max(mpg), mpg_mean = mean(mpg), mpg_max2 = max2(mpg))
# A tibble: 2 × 4
     am mpg_max mpg_mean mpg_max2
  <dbl>   <dbl>    <dbl>    <dbl>
1     0    24.4     17.1     22.8
2     1    33.9     24.4     32.4


2Lの数字を変えれば、n番目の数字に対応します。

【R】とりあえず簡単にggpplot2で2軸目を書きたい時はsec.axis

R 備忘録 R データ分析

数ヶ月に一回ググってる気がするので自分用にメモ。

問題

とりあえずggplot2でエクセル的な2軸プロット（左右に別のY軸があってグラフが重なってるやつ）を書きたい。
ググっても丁寧なブログはたくさん見つかるのだが、とりあえずどれやればいいの！となる。
ggplot2以外に追加的にパッケージとかも使いたくない。

解決策

sec.axisをscale_y_continuous()で使う。

# 適当な例
ggplot(data, aes(x=x,y=y, col=group)) +
   geom_line()+
   scale_y_continuous(sec.axis=sec_axis(~.*10, name="y2")) #ココ！

解説

準備

標準装備airqualityのデータを例に使います。

# パッケージ
library(tidyverse) # ggplot2含む

# データロード
data(airquality) 

# 時系列データにするためにDate変数を作成
airquality = airquality %>%
  # 元データに月と日はあり（MonthとDay）。年は適当に今年になる。
  mutate(date = as.Date(paste(Month,Day,sep="-"), format="%m-%d"))

ステップ１：とりあえず描画

ワイドデータ（異なる変数がそれぞれの列で記録されているデータ）をそのまま描画する場合です。
ロングデータ（変数の値が一つの列に記録され、もう一つの列に変数名やカテゴリが記録されてるようなデータ）は後述。

まずとりあえずデータをそのまま描画すると以下のようになる。

ggplot(data=airquality,
       aes(x=date)) +
  geom_line(aes(y=Wind,col="Wind"))+
  geom_line(aes(y=Temp,col="Temp"))


なんかちょっと離れてるので重ねたい、みたいなときありますよね。

ステップ２：スケールする

一方の変数に係数をかけたり足し引きしたりすることでスケールする。
このスケールは、使うデータによるので、ここは数字みながら試行錯誤する必要ありです。
今回はシンプルに２つ目の変数である温度(temp)の数値が高いのでいい感じの数を引いてます。

# トライ2 スケールする
ggplot(data=airquality,
       aes(x=date)) +
  geom_line(aes(y=Wind,col="Wind"))+
  geom_line(aes(y=Temp-70,col="Temp"))


ステップ３：２軸目を足す

ここが一番の肝。
scale_y_continousの中でsec.axisという引数を使う。
このときに、sec_axisという関数で、数値をスケールすることができる。
上で70引いているので、ここでは70を足すことで本来の数値を表示できる。

# トライ3 2軸目を足す
ggplot(data=airquality,
       aes(x=date)) +
  geom_line(aes(y=Wind,col="Wind"))+
  geom_line(aes(y=Temp-70,col="Temp"))+
  scale_y_continuous(sec.axis = sec_axis(~.+70)) # ２軸目のY軸


ステップ４：２軸目のラベルを足す

２軸目がなんなのか表示する。
nameという引数で表示できるが、sec_axis関数の中でつかうこと！
カッコを見間違えてsec_axisの外、scale_y_continuousの引数としてnameを使うと、エラーが返されずに第１軸のラベルとして認識されてしまう。
２軸だと単位が異なる事が多いので、軸ラベルに単位を明示すると丁寧ですよね。

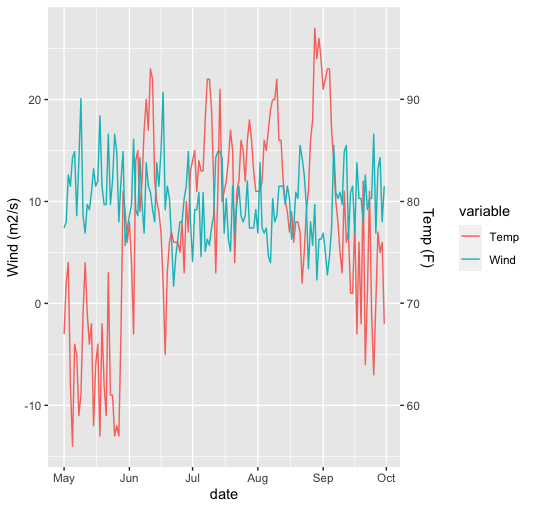
ggplot(data=airquality,
       aes(x=date)) +
  geom_line(aes(y=Wind,col="Wind"))+
  geom_line(aes(y=Temp-70,col="Temp"))+
  scale_y_continuous(sec.axis = sec_axis(~.+70, 
                                         name="Temp (F)"),
                     name="Wind (m2/s)"
                     )

なんでこんな気温高いんだと思ったら華氏（F）だからでした。

さらに細かくカスタマイズしたりスケールを設定するには「ggplot ２軸」とかで検索するとたくさんひっかかるのですが、とりあえず２軸！じゃあsec.axis！というのを覚えるために書きました。

おまけ：ロングデータ

ggplotだとロングデータ使って、color引数とかでカテゴリを色分けすることとか多いんですが、その場合はデータに予めスケールをかけとくほうがいいかもです。

以下はロングデータとワイドデータの違い。今回はOzoneとSolar.Rは無視してます。

#ロングデータに変換
airquality_long = airquality %>%
  pivot_longer(cols=c(Temp,Wind),names_to = "variable",values_to = "value")

# ロングデータ
> head(airquality_long)
# A tibble: 6 × 7
  Ozone Solar.R Month   Day date       variable value
  <int>   <int> <int> <int> <date>     <chr>    <dbl>
1    41     190     5     1 2022-05-01 Temp      67  
2    41     190     5     1 2022-05-01 Wind       7.4
3    36     118     5     2 2022-05-02 Temp      72  
4    36     118     5     2 2022-05-02 Wind       8  
5    12     149     5     3 2022-05-03 Temp      74  
6    12     149     5     3 2022-05-03 Wind      12.6

#ワイドデータ
> head(airquality)
  Ozone Solar.R Wind Temp Month Day       date
1    41     190  7.4   67     5   1 2022-05-01
2    36     118  8.0   72     5   2 2022-05-02
3    12     149 12.6   74     5   3 2022-05-03
4    18     313 11.5   62     5   4 2022-05-04
5    NA      NA 14.3   56     5   5 2022-05-05
6    28      NA 14.9   66     5   6 2022-05-06

スケールした新しい変数を作成

airquality_long = airquality_long %>%
  # もしvariableがTempなら70引く
  mutate(value2 = ifelse(variable=="Temp",value-70,value))

通常のggplot2の文法で書く。このときvalueではなくvalue2をy変数にセットする。
２軸の書き方は上と全く同じです。

ggplot(data=airquality_long,
       aes(x=date,y=value2,col=variable)) +
  geom_line()+
  scale_y_continuous(sec.axis = sec_axis(~.+70, 
                                         name="Temp (F)"),
                     name="Wind (m2/s)"
  )

【R】geom_sfで地図描こうとしたらst_cast.POINTというエラーが出た。

R 備忘録 R データ分析

またしても備忘録

問題

ggplotを使ってsfオブジェクトを描画しようとすると以下のエラーが出た。

Error in st_cast.POINT(x[[1]], to, ...) :
cannot create MULTILINESTRING from POINT

解決策

球形幾何のパッケージであるs2が有効になっていると起こる問題であるらしい。
s2を無効にしてやればとりあえず問題は解決する。

sf_use_s2(FALSE)

参考

github.com


地理空間データの扱い方もアドホックな使い方ではなく、きちんと勉強したいなぁ。。

実践Data Scienceシリーズ Rではじめる地理空間データの統計解析入門 (KS情報科学専門書)

実践Data Scienceシリーズ Rではじめる地理空間データの統計解析入門 (KS情報科学専門書)

Amazon