回帰分析で変数の対数を取る理由はなんでだっけ?
回帰分析をやっていてふと基本的な疑問にひっかかった。
なぜ、そしていつ変数の対数変換をやるのか?
統計学や計量経済学をやった人には基本的なこの質問なのだが、復習ということで本やウェブを漁った備忘録を残しておく。
対数変換とは?
対数変換とは文字通り、変数の対数を取ることである。ことわりがない限り、自然対数を意味している場合が多い。
つまり対数の底がネイピア数(Napier's constant)である。
ある変数Xに対して、が対数変換である。自然対数はよく
と表記される。
回帰分析の対数変換
ある従属変数Yに対する説明変数Xの影響を測りたい場合に以下のような線形のモデルを使用する。
説明変数・従属変数、そして両方を対数変換する場合として以下の3つのバリエーションが有る。
このとき、パラメータの解釈が異なることに注意である。
- 線形ー対数モデル linear-log
このとき、 はXが1%増加したとき、Yがいくら(もとの単位で)増加するかを示す。
- 対数ー線形モデル log-linear
ここでは逆に、 はXが1単位増加したとき、Yが何%増加するかを示す。
- 対数ー対数モデル log-log
この場合はは後述する弾力性と呼ばれるもので、Xが1%増加したときにYが何%増加するかを示す。
経済学ではlog-linearとlog-logをよく見る印象である。
なぜ対数変換を行うのか?
なぜわざわざ対数変換を行うのか?これにはいくつかの理由がある。
基本的には変数の性質と回帰分析の仮定の問題、そして推定パラメータの解釈の問題だ。
1. 非線形な関係を線形モデルで表す。
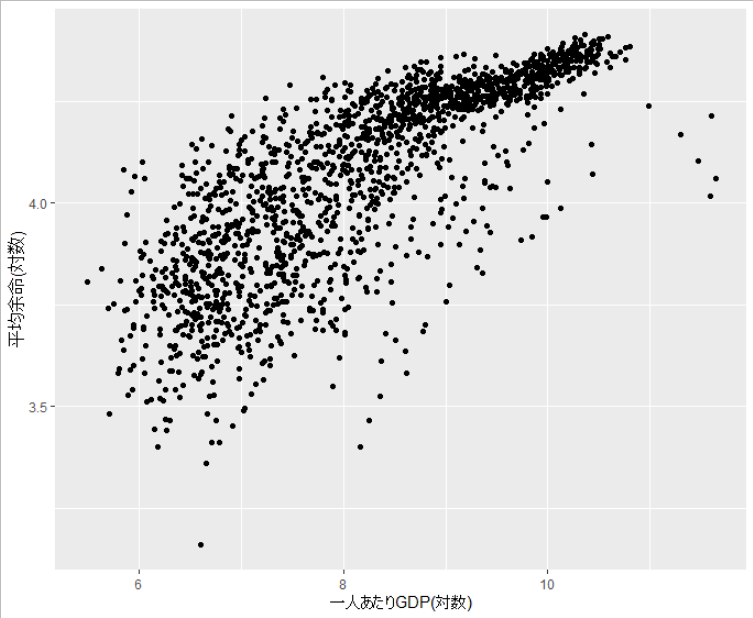
たとえば説明変数が増加するにつれ、従属変数も増加するがその増加率が一定でない場合、線形モデルを当てはめるのは適当ではない。
今話題の新型コロナウイルス感染症、COVID-19の患者数増加グラフもその一例で、Y軸を見ればわかるように底が10の対数を取っている。

ここではgapminderのデータを使ってRで例示してみる。
library(gapminder) library(ggplot2) # 平均寿命と一人あたりGDP ggplot(gapminder, aes(x =gdpPercap, y = lifeExp))+ geom_point() + labs(x = "一人あたりGDP", y = "平均余命")

その場合に、対数変換を行う。
ggplot(gapminder, aes(x =log(gdpPercap), y = log(lifeExp)))+ geom_point() + labs(x = "一人あたりGDP(対数)", y = "平均余命(対数)")
2. 変数の分布が偏っている。
変数の分布が正規分布でない場合、回帰分析の推定や統計的検定のための仮定が成り立たなくなる。
ggplot(gapminder, aes(x = gdpPercap)) + geom_histogram() + labs(x = "一人あたりGDP", y= "頻度")
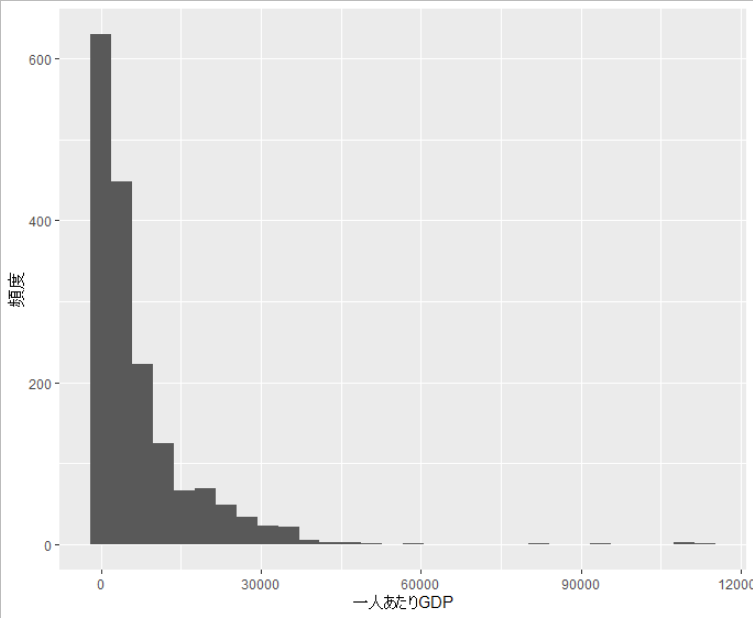
対数変換することによって、分布が正規分布に近くなる。
特に正の値しか取らない変数の場合は、分布が偏っている事が多いため、対数を取ることが多い。(例えば賃金)
また、そういった場合は回帰分析後の予測値が0以下にならないという利点もある。
ggplot(gapminder, aes(x = log(gdpPercap))) + geom_histogram() + labs(x = "一人あたりGDP(対数)", y= "頻度")
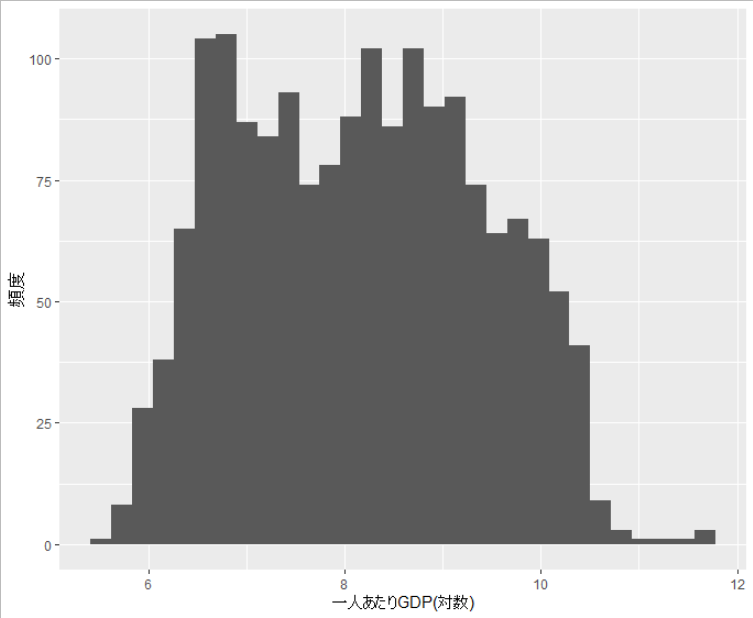
3. 極端な数値の効果を低減する
もしデータに極端に大きい・小さい数値が含まれていても、その影響を軽減できるという効果もある。
たとえばlog(100)は4.60517で、log(10000)は9.21034になる。
4. 推定パラメータの解釈
推定されたパラメータの解釈は、対数変換したかどうか、またどの変数を対数変換したかどうかによって変わる。
特に経済学などでは、弾力性の推定に興味がある場合に、対数ー対数モデルで推定したパラメータが弾力性そのものであるため、
対数ー対数モデルを多く使用する傾向がある。しかし、これは1点目の変数間の関係に依存している。
つまり、経済学的に弾力性を推定したい、という場合は、明示されていなくても暗示的に対数ー対数モデルになるような変数関係があると仮定されている。
ちなみに弾力性(elasticity)とは、変数同士の関係で、ある変数の変化率に対する別の変数の変化率を表したものである。具体的にはある変数が1%変化した場合にもう一方の変数が何%変化するか?という数値が弾力性である。
経済学で一般的なのは需要の価格弾力性である。価格が1%上がったときに、需要が何%減少するか?を推定するときに(内生性などは置いといて)、対数を取った需要量と価格を使って回帰式を推定すれば、推定されたパラメータが、価格弾力性そのものになる。
なぜか?
価格弾力性を数式で定義すると以下の様になる。
つまりdQはQの変化量なので、dQ/Qは需要量Qが何%変化したかを表す。Pも同様である。
そして、上の回帰式を全微分する。
これをアレンジすると
となるので、が価格弾力性となるという論理である。
5. 経済モデルから導かれた式の推定
これは3の理由に近いが、経済モデルから導かれたモデル式を推定するのに、対数変換すると線形になって推定しやすいから、というのがある。
経済学でよく使われるコブ・ダグラス関数系の生産関数を例にすると
という関数があるとする。ここでAは技術、Kは資本、Lは労働を表すとする。
仮に資本と労働のデータがあったとしても、このままでは線形回帰はできない。
そこで、両辺の対数を取って誤差項を加えると
となるので、線形回帰を行うことで、と
が推定できる。
まとめ
まとめると、回帰分析で変数の対数を取るかどうかは変数そのものの性質(正の値しか取らない、分布の偏り)と、変数同士の関係(線形か非線形か)をある程度考えた上で決める。
さらに、経済学などのモデルから推定式を得られる場合はモデル解釈の都合から対数を取る。
しかし、これらは独立した理由ではなくそれぞれ関係した理由である。たとえばコブダグラスのモデルのパラメーターはそれ自体は弾力性なので、log-logで推定することに正当性があるし、
正の値しか取らないような変数は特にゼロ付近で他の変数と線形関係があるとは言えない場合が多い、などである。
機械的に対数を取るかどうか、ではなく事前のデータの理解と、推定したい仮説やモデルが重要になるということだろう。
参考
Wooldridge, Introductory Econometrics
http://fmwww.bc.edu/ec-c/F2007/228/EC228.f2005.nn06.pdf
Benoit, Linear Regression Models with Logarithmic Transformations
https://kenbenoit.net/assets/courses/ME104/logmodels2.pdf
福井県立大学、経済統計学のノート
http://www.s.fpu.ac.jp/u-sano/macro/log01.pdf